(ES6) Number.EPSILON은 왜 2.220446049250313e-16인가?

작성일 In , , Disqus:

들어가기에 앞서

  1. Number.EPSILON이 뭔지 모르는 사람은 해당 링크를 참조하고 오자.
  2. 부동소수점이 뭔지 모르는 사람은 해당 링크를 참조하고 오자.

자바스크립트에서 숫자의 자료형은?

C나 Java를 접해본 사람이라면 숫자의 자료형은 크게 두 가지로 나눌 수 있을 것이다.

  1. 정수
  2. 실수

하지만 자바스크립트에서는 실수 하나 밖에 존재하지 않는다.

1
2
3
console.log(0 === 0.0); // true
console.log(0 === .0); // true
console.log(.0 === 0.0); // true

또 이 실수는 크게 두 가지로 나눌 수 있을 것이다.

  1. float
  2. double

하지만 자바스크립트에서는 이 실수형 중에서도 double 형 하나 밖에 존재하지 않는다.

실수를 나타내는 데도 고정 소수점과 부동 소수점이 존재하는데 고정소수점은 직관적인데 반해 표현할 수 있는 범위가 좁아서
거의 부동 소수점이 실수를 표현하는데 표준으로 자리잡고 있다.
물론 이 부동 소수점도 오차가 존재한다는 단점을 떠안고 있지만…

이 부동 소수점을 표현하는데도 여러가지 방법이 있는데(아마도…?) 현재 거의 표준으로 자리잡은 것은
전기 전자 기술자 협회(IEEE)에서 제정한 IEEE754라는 것이다.

double 형이란…?

자바스크립트도 이 IEE754를 따라서 숫자(실수, 부동소수점)을 표현하고 있고,
Double-precision floating-point format을 따르고 있다.

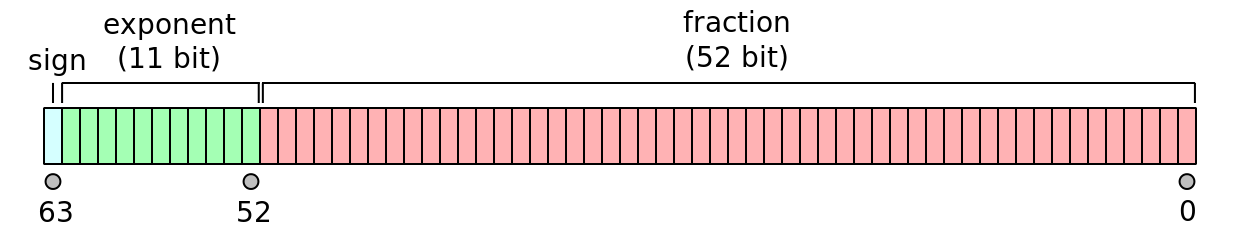
해당 부동소수점 표현 방식은 아래와 같이 세 가지 부분으로 나뉘어진다.

  1. 부호 비트(sign, 1bit)
    MSB(most significant bit): 최상위 비트, 즉 제일 왼 쪽에 있는 비트를 뜻하며 0이면 양수, 1이면 음수를 나타낸다.
  2. 지수부(exponent, 11bit)
    이진 소수를 정규화 했을 때 나타낼 지수부.
    지수부는 정수형과 달리 바이어스 표기법을 사용한다.
    범위는 -211-1-1 ~ 211-1, 즉 -21024-1 ~ 21024이다.
    해당 범위를 넘어가는 지수부에 한해서는 아마도 오버플로우가 발생해서 예기치 않은 결과를 뿜어내지 않을까 싶다.(NaN, ±Infinity)
    또한 지수 표기법과 같이 1e1 같은 숫자를 봤을 때 나오는 저 e가 지수부의 exponent를 줄인 것이다.
  3. 가수부(fraction, 52bit)
    이진 소수를 정규화 했을 때 나타낼 가수부.
    부호 없는 정수를 나타내는 방식과 동일하며 0252-1 = 0 ~ 4503599627370495이다.
    4503599627370495는 십진수 16자리인데 0    15자리 수를 모두 커버하고 있으므로 double의 정밀도는 소수점 15자리가 되는 것이다.

부동 소수점은 먼저 아래와 같은 절차를 거친다.

  1. 십진 소수를 이진 소수로 바꾼다. (십진 소수 8.25를 이진 소수로 바꾸면 1000.01(2))
  2. 이진 소수를 정규화한다. (이진 소수를 지수부와 가수부로 나누어서 표현한 방식을 뜻한다.)
    예를 들어 이진 소수 1000.01(2)을 정규화를 거치면 1.000101(2) X 103(2)와 같이 나타나며 1.101e3(2)로도 표현이 가능하다.

물론 지수부의 범위를 넘어서는 숫자라면 오버플로우가 발생할 것이고 가수부의 범위를 넘어서는 경우에는 오차가 발생한다.
이 오차는 왜 발생할까?

  1. 가수부의 범위를 넘어서는(정규화 이후에 소수점 이하가 15자리를 넘어서는 경우) 경우
  2. 십진수로는 유한 소수인데 이진수로는 무한 소수인 경우
    0.1만 해도 이진수로는 표현이 불가능하다. (구해보면 이진수로는 무한 소수)
    따라서 끝자리가 5로 끝나는 소수가 아니면 유한소수라고 단정지을 수가 없고, 오차가 없다고 말할 수가 없다.

왜 Number.EPSILON은 2.220446049250313e-16일까?

double 형 부동 소수점 가수부에서 0을 제외하고 가장 작은 숫자는 무엇일까?
바로 2-52, 0.0000000000000002220446049250313(2.220446049250313e-16)이다.
(가수부는 소수점 이하를 표현하는 것이기 때문에 252가 아니다.)
그 말은 0 < x < 0.0000000000000002220446049250313, 즉 x는 표현하지 못하는 숫자가 된다.
그래서 Number.EPSILON이 2-52, 즉 2.220446049250313e-16가 된 것이다.